The player is at position (playerX, playerY), and an enemy is at (enemyX, enemyY). You want the enemy to move 5 units directly toward the player. A lot of times, you'll see people do:
dx = player.x - enemy.x;
dy = player.y - enemy.y;
angle = Math.atan2( dy, dx );
speedX = 5 * Math.cos( angle );
speedY = 5 * Math.sin( angle );
enemy.x += speedX;
enemy.y += speedY;
It took us three hefty trigonometry operations: atan2, sin, and cos. First, we're going from the x and y components (dx and dy) to the angle using atan2. Then we're going BACK to the components using sin and cos! Surely we can avoid running in a circle like this! (haha, in a circle, get it?)
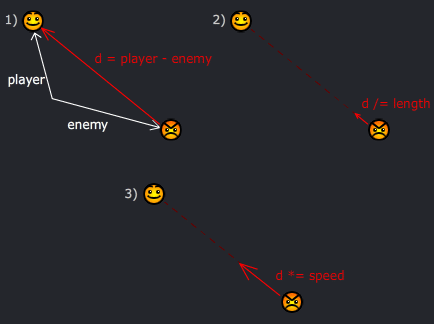
It's a little easier if you think with vectors. We already have a vector pointing in the direction we want: the <dx, dy> vector points straight from the enemy to the player! All we have to do is resize it to our desired speed.
dx = player.x - enemy.x;
dy = player.y - enemy.y;
length = Math.sqrt( dx*dx + dy*dy );
dx /= length; dy /= length; // normalize (make it 1 unit length)
dx *= 5; dy *= 5; // scale to our desired speed
enemy.x += dx;
enemy.y += dy;
We normalize the vector by dividing it by its length. Now our vector has a length of one unit, so we can scale it by our desired speed. Instead of three trig functions, we now have just a sqrt!
It's common to rotate your enemy to face the player. In this case, you DO want to use atan2 to get the angle. You can still avoid the sin and cos, though, by doing what we did above.
Just thought I'd share this little tip, hope it's helpful to someone. Here's a bad diagram:
MaestroRage
That was easy enough for me to understand, and that means it's awesome. Thanks.